[자료구조&알고리즘] 최소비용신장트리(Prim, Kruskal, Dijkstra 알고리즘)

: 무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리

🧩프림 알고리즘 (Prim Algorithm)

목적: 그래프의 모든 정점을 최소 비용으로 연결하는 최소 신장 트리(MST, Minimum Spanning Tree)를 찾는 것.
적용 과정:
1. 임의의 시작 정점을 선택해 트리를 시작한다.
2. 현재 트리에 인접한 간선들 중에서 가중치가 가장 작은 간선을 선택한다.
3. 해당 간선의 반대편 정점을 트리에 추가한다.
4. 모든 정점이 포함될 때까지 2~3단계를 반복한다.

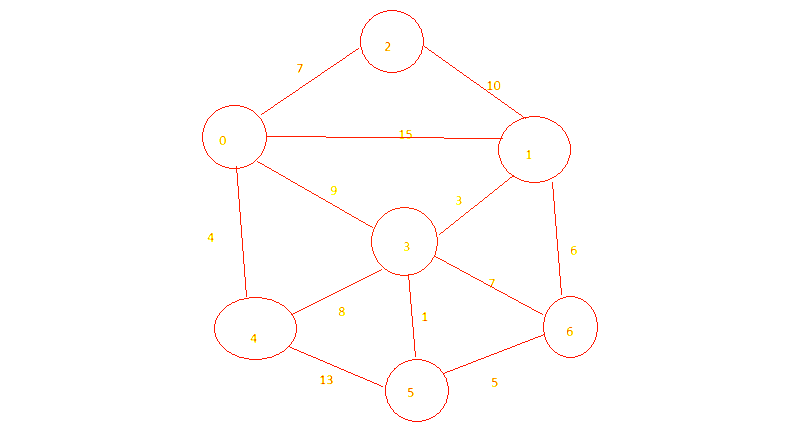
초기 상태:

임의의 시작 정점: 0
방문한 정점: {0}
후보 간선: 0에서 연결된 모든 간선들

1단계: 첫 번째 간선 선택

정점 0에서 연결된 간선들:

(0,2): 가중치 7
(0,1): 가중치 15
(0,3): 가중치 9
(0,4): 가중치 4 ← 최소값, 선택

선택된 간선: 0-4 (가중치 4)
방문한 정점: {0, 4}
누적 가중치: 4

2단계: 두 번째 간선 선택

현재 방문한 정점들 {0, 4}에서 미방문 정점으로 가는 간선들:

(0,2): 가중치 7 ← 최소값, 선택
(0,1): 가중치 15
(0,3): 가중치 9
(4,3): 가중치 8
(4,5): 가중치 13

선택된 간선: 0-2 (가중치 7)
방문한 정점: {0, 4, 2}
누적 가중치: 4 + 7 = 11

3단계: 세 번째 간선 선택

현재 방문한 정점들 {0, 4, 2}에서 미방문 정점으로 가는 간선들:

(4,3): 가중치 8 ← 최소값, 선택
(0,3): 가중치 9
(2,1): 가중치 10
(0,1): 가중치 15
(4,5): 가중치 13

이런식으로 하면...

결과

Prim 알고리즘에 의해 선택된 처음 3개의 트리 간선:

0-4 (가중치 4)
0-2 (가중치 7)
4-3 (가중치 8)
(3-5, 1)
(3-1, 3)
(5-6, 5)

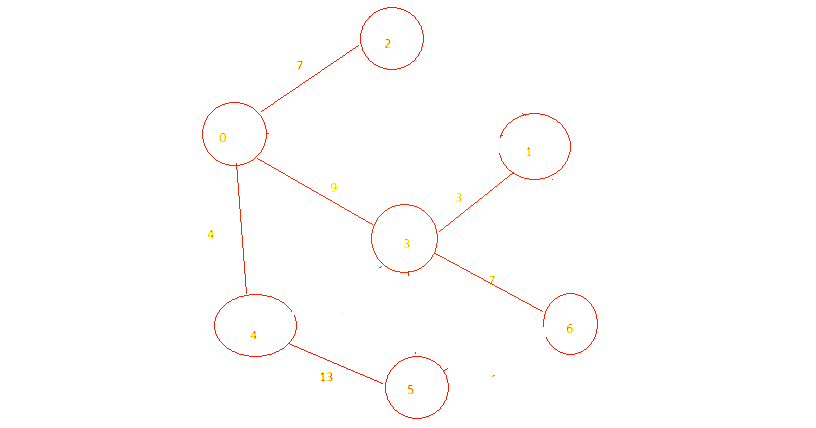
특징:
- 항상 하나의 트리 집합을 유지하며, 트리를 점차 확장.
- 인접한 간선만 선택(로컬 확장).
- 우선순위 큐(힙)를 사용해 효율적으로 구현 가능.
적용 예: 네트워크 케이블 최소 비용 연결 등.

🧩크루스칼 알고리즘 (Kruskal Algorithm)

목적: 그래프의 모든 정점을 최소 비용으로 연결하는 최소 신장 트리(MST)를 찾는 것.
적용 과정:
1. 그래프의 모든 간선을 가중치 기준으로 오름차순 정렬한다.
2. 가장 가중치가 작은 간선부터 하나씩 선택한다.
3. 사이클이 생기지 않는 경우에만 간선을 MST에 추가한다.
4. n-1개의 간선이 선택될 때까지 2~3단계를 반복한다.

1. 3-5 (1)

선택 (사이클 없음)
MST: 3-5

2. 1-3 (3)

선택 (사이클 없음)
MST: 3-5, 1-3

3. 0-4 (4)

선택 (사이클 없음)
MST: 3-5, 1-3, 0-4

4. 5-6 (5)

선택 (사이클 없음)
MST: 3-5, 1-3, 0-4, 5-6

5. 1-6 (6)

1과 6은 현재
- 1-3-5-6으로 연결됨(1-3, 3-5, 5-6)
- 1-6을 선택하면 사이클 생김 → 선택하지 않음

6. 0-2 (7)

0과 2는 아직 연결 안 됨
선택 (사이클 없음)
MST: 3-5, 1-3, 0-4, 5-6, 0-2

7. 3-6 (7)

3과 6은 이미 3-5-6으로 연결됨
선택하면 사이클 생김 → 선택하지 않음

8. 3-4 (8)

3과 4는
- 3-5-6, 1-3, 0-4, 0-2
- 3과 4는 아직 MST 상에서 연결 안 됨
- 선택 (사이클 없음)
MST: 3-5, 1-3, 0-4, 5-6, 0-2, 3-4

이 시점에서 간선 개수 = 정점 개수 - 1 = 7 - 1 = 6개
→ MST 완성!

최소 신장 트리(MST)

간선 및 가중치:

3-5 (1)
1-3 (3)
0-4 (4)
5-6 (5)
0-2 (7)
3-4 (8)

총 가중치: 1 + 3 + 4 + 5 + 7 + 8 = 28

이 시점에서 간선 개수 = 정점 개수 - 1 = 7 - 1 = 6개
→ MST 완성!

특징:
- 항상 하나의 트리 집합을 유지하며, 트리를 점차 확장.
- 인접한 간선만 선택(로컬 확장).
- 우선순위 큐(힙)를 사용해 효율적으로 구현 가능.
적용 예: 네트워크 케이블 최소 비용 연결 등.

🧩다익스트라 알고리즘 (Dijkstra Algorithm)

목적: 한 정점에서 다른 모든 정점까지의 최단 경로(Shortest Path)를 찾는 것.
적용 과정:
1. 시작 정점에서 각 정점까지의 거리를 무한대로 초기화(시작점은 0).
2. 방문하지 않은 정점 중 최단 거리가 가장 짧은 정점을 선택한다.
3. 해당 정점의 인접 정점까지의 거리를 계산해, 기존 값보다 작으면 갱신한다.
4. 모든 정점을 방문할 때까지 2~3단계를 반복한다.

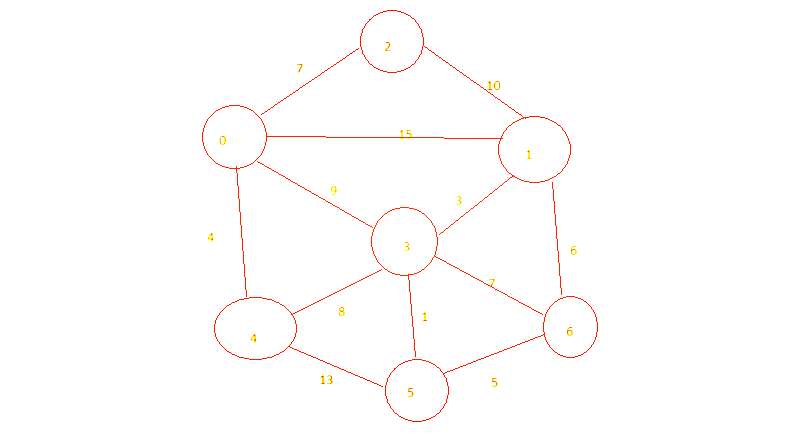
최단 경로 및 거리:

0 → 0 : 0 (자기 자신)
0 → 1 : 0-3-1, 9+3 = 12 (0-1 직접(15)보다 짧음)
0 → 2 : 0-2, 7
0 → 3 : 0-3, 9
0 → 4 : 0-4, 4
0 → 5 : 0-3-5, 9+1 = 10
0 → 6 : 0-3-5-6, 9+1+5=16

최단 경로 그림

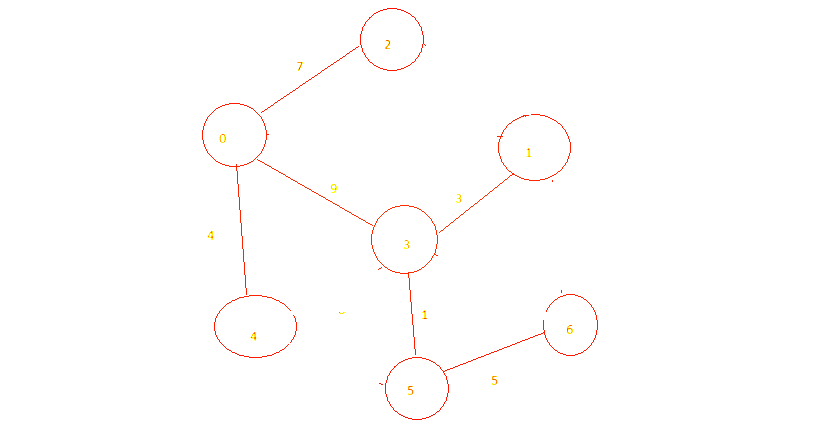
0-4 (4)
0-2 (7)
0-3 (9)
3-1 (3)
3-5 (1)
5-6 (5)

최단 거리 요약

0→1: 12
0→2: 7
0→3: 9
0→4: 4
0→5: 10
0→6: 15

특징:
- "최단 거리" 기준으로 노드를 선택하며, 경로 누적 거리를 계속 비교·갱신.
- MST가 아니라, 한 점에서 다른 점까지의 경로에 초점.
- 간선 가중치는 반드시 0 이상이어야 함(음수 불가).
적용 예: 네비게이션, 지도 앱, 통신 경로 계산 등.

📒요약

알고리즘	목적	적용 과정 /기준	결과	비고
프림	최소 신장 트리(MST)	트리 확장, 인접 간선	모든 정점 최소 비용 연결	하나의 트리 유지
크루스칼	최소 신장 트리(MST)	간선 정렬, 사이클 방지	모든 정점 최소 비용 연결	여러 트리 합치며 진행
다익스트라	단일 출발점 최단 경로	누적 최단 거리 갱신	출발점~각 정점 최단 경로	음수 가중치 불가, MST 아님

참고

프림과 크루스칼은 MST(최소 신장 트리) 알고리즘이지만, 트리 확장 방식(프림: 하나의 트리 확장 / 크루스칼: 여러 트리 합침)이 다릅니다.
다익스트라는 한 정점에서 다른 정점까지의 최단 경로를 구하는 알고리즘으로, MST와 목적이 다릅니다.

핵심:

프림/크루스칼: MST(최소 신장 트리)
다익스트라: 단일 출발점 최단 경로

Citations:

'자료구조&알고리즘' 카테고리의 다른 글

[자료구조&알고리즘] 트리(Tree) (0)	2025.05.24
[자료구조&알고리즘] 탐색(Search) (1)	2025.05.23
[자료구조&알고리즘] 정렬(Sort) (0)	2025.05.04

🧩프림 알고리즘 (Prim Algorithm)

🧩크루스칼 알고리즘 (Kruskal Algorithm)

🧩다익스트라 알고리즘 (Dijkstra Algorithm)

📒요약

참고

핵심:

'자료구조&알고리즘' 카테고리의 다른 글

티스토리툴바